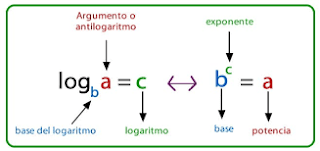
DEFINICIÓN:
Un logaritmo indica el exponente por el cual se debe elevar la base para obtener la potencia indicada, de manera que esta es la relación entre un logaritmo y una potencia.
- Exponente = logaritmo
- Potencia = número
- Base de la potencia = base del logaritmo
EJEMPLO:
Para expresar, un logaritmo de 9 en base 3 que es igual a 2 sería:
![]()
El logaritmo expresado significa que 3 elevado a 2 es igual 9:
![]()
LOGARITMOS DECIMALES:
Cuando la base del logaritmo no parece expresada es 10.
LOGARITMOS NEPERIANO:
Cuando la base del logaritmo es e, expresión matemática que indica 2.718281828. Es un procedimiento similar a los logaritmos en otra cualquier base.
EJERCICIOS:
PROPIEDADES DE LOGARITMOS
Hay tres tipos de propiedades de logaritmos importantes:
1. PROPIEDAD
El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
2.PROPIEDAD
El logaritmo de un cociente es igual al logaritmo del dividiendo menos el logaritmo del divisor

3.PROPIEDAD
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base

Aunque cabe destacar que existen dos propiedades más, las cuales no hemos estudiado en clase pero a continuación las mostraré
4.PROPIEDAD
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz

5.PROPIEDAD
Cambio de base:
- No existen logaritmos de un número con base negativa
- No existen logaritmos de un número negativo
- No existen logaritmos de 0
- El logaritmo de uno es igual a 0
- El logaritmo de a en base a es igual a 1
- El logaritmo en base a de una potencia en base a es igual al exponente
- El logaritmo de un producto es igual a la suma de los logaritmo de los factores
- El logaritmo de un cociente es igual a logaritmo del dividiendo menos el logaritmo del divisor
- El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base
- El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz
REPRESENTACIÓN GRÁFICA:
Dichas raíces las podemos encontrar representadas en gráficos
- Si la curva rebota en la línea de abajo sígnica que esa raíz esta elevado al cuadrado, es decir se denomina raíz doble porque se repite.
- Si la linea toca el eje de las X de manera vertical, quiere decir que es raíz.
- Si la curva no toca la línea significa que no puede ser factorizado.
Ejemplos:
En la recta de la izquierda podemos apreciar como rebota, por tanto, tiene raíz doble. Mientras que en la de la derecha vemos como pasa por el dos, por tanto, dicho es una raíz.






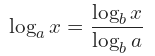


No hay comentarios:
Publicar un comentario