¿Qué es el límite de una función?
Se representa de la siguiente manera:
![]()
Que significa, tal y como te acabo de decir, que cuando X tiende al punto Xo, el valor de la función se va aproximando a L, por tanto, el límite de esa función cuando X tiende a Xo es L. Gráficamente quedaría de la siguiente manera:
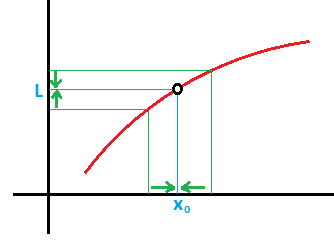
Si te das cuenta, conforme nos vamos aproximando al valor Xo en el eje x, en el eje y, el valor de la función se va a aproximando al valor L.
x puede tender a cualquier valor, desde menos infinito hasta más infinito (ambos incluidos) y el límite de una función también puede ser desde menos infinito hasta infinito (ambos incluidos).
No hay que confundir el límite de una función con el valor de una función en punto, que es el valor que tiene la función justo en ese punto. Mucho cuidado porque pueden no coincidir (lo veremos más adelante).
Vamos a verlo con un ejemplo.
¿Cuál es el límite de la siguiente función:
![]()
cuando x tiende a -1?
El límite de la función cuando x tiende a -1 se escribe:
![]()
Para que entiendas como el valor de la función se va a aproximando a un valor determinado, mientras que x va tendiendo a -1, vamos a ir viendo cuál es el valor de la función para los puntos que próximos a -1 y cada vez nos vamos a ir acercando más a -1.
Primero nos vamos a ir acercando cada vez más a -1 por la izquierda a ver qué pasa.
Cuando x=-1,3, el valor de la función es:
![]()
Cuando x=-1,2, el valor de la función es:
![]()
Cuando x=-1,1, el valor de la función es:
![]()
Si te das cuenta, conforme nos vamos acercando a -1, el valor de la función se va aproximando a 0.
Vamos hacer lo mismo ahora, pero acercándonos al 1 por la derecha.
Cuando x=-0,7, el valor de la función es:
![]()
Cuando x=-0,8, el valor de la función es:
![]()
Cuando x=-0,9, el valor de la función es:
![]()
Como puedes observar, conforme nos vamos acercando a x=-1 por la derecha, la función se va aproximando cada vez más a 0.
Si lo vemos en una gráficamente, vemos como la gráfica de la función se aproxima al punto 0 en el eje y, cuando los valores de x se van a aproximando al punto -1 en el eje x:

Por tanto, el límite de la función cuando x tiende a -1 es igual a 0:
![]()
Para resolver un límite no es necesario realizar este procedimiento que acabamos de hacer. Tan solo lo he hecho para que fueras viendo cómo poco a poco el valor de la función se va aproximando a un punto.
Resolver el límite de esa función es mucho más sencillo y es lo que te voy a explicar en el siguiente apartado.
Para complementar:
Fórmula del número e
El número e se expresa mayoritariamente por la letra e. También podemos encontrarlo como una función exponencial cuando la variable es igual a 1:
La gente que sabe está en el Campus
Para que aprendas mucho más sobre finanzas, inversión y bolsa, hemos creado el Campus de Economipedia. Una plataforma de cursos en vídeo, pensada para que aprendas de forma entretenida con contenidos prácticos y entretenidos.
Los primeros 1.000 suscriptores tienen un 50% de descuento de por vida, ¡aprovéchalo!

Los 40 primeros decimales del número e son:

El número e y los límites
Tenemos que pensar en un límite de una función determinada cuando queramos entender el origen matemático del número e:
Esta función es una sucesión tal que:

Hablamos de sucesión porque podemos asignar valores ordenados a la variable n.
- Para n= 20 tendremos f(20) = 2,65329
- Para n=100 tendremos f(100) = 2,7048
Podéis ver que a medida que incrementamos el valor de n, es decir, incrementamos la longitud de la sucesión, más se acerca el resultado de la función al número e. ¿Qué pasará para n = 10 000?
- Para n= 10 000 tendremos f(10 000) = 2,718146
La expresión matemática generalizada de la sucesión sería teniendo en cuenta que n se aproxima a infinito. En el siguiente gráfico se puede ver como la sucesión (línea negra) va acercándose al límite (línea azul), es decir, al número e, a medida que aumenta n.

Por tanto, a medida que n se aproxima a infinito, la función, es decir, f(n), se va colapsando en el número e, es decir, 2,7181.

Entonces, podemos entender el número e como un límite de una sucesión:

Aplicación
El número e aparece numerosas veces en los campos de cálculo, análisis matemático, teoría de números, estadística y geometría. También aparece en la disciplina de las finanzas, concretamente, en el cálculo de la rentabilidad continua o el interés continuo.

Ejemplo
Escribir dos fórmulas que contengan el número e.
Por ejemplo, podemos pensar en la función de densidad de la distribución normal (1) y, en el ámbito de los números complejos, podemos encontrar la identidad de Euler (2), formulada a través del número e:


No hay comentarios:
Publicar un comentario